Multiclass Diffential Expression Analysis
May 31, 2017
Multi-class / Multi-group Differential Expression Analysis
Introduction
In transcriptomics analysis, we are often interested in identifying differentially expressed genes. For example, if we have two conditions or cell types, we may be interested in what genes are significantly upregulated in condition A vs. B or cell type X vs. Y and vice versa. However, what happens when you have multiple conditions or many cell types? In this tutorial, I will use simulated data to demonstrate potential stategies for performing multi-class or multi-group differential expression analysis.
Simulation
First, let’s simulate 5 different classes/groups of samples (say, bulk RNA-seq of 5 different sorted cell types), each with 30 samples each, each expressing 1000 genes total. Note, in this very simplistic demonstration, we will assume that our gene expression follow a normal distribution.
set.seed(0)
G <- 5
N <- 30
M <- 1000
initmean <- 5
initvar <- 10
mat <- matrix(rnorm(N*M*G, initmean, initvar), M, N*G)
rownames(mat) <- paste0('gene', 1:M)
colnames(mat) <- paste0('cell', 1:(N*G))
group <- factor(sapply(1:G, function(x) rep(paste0('group', x), N)))
names(group) <- colnames(mat)
heatmap(mat, Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
Now, let’s simulate some differentially upregulated genes unique to each group.
set.seed(0)
upreg <- 5
upregvar <- 10
ng <- 100
diff <- lapply(1:G, function(x) {
diff <- rownames(mat)[(((x-1)*ng)+1):(((x-1)*ng)+ng)]
mat[diff, group==paste0('group', x)] <<- mat[diff, group==paste0('group', x)] + rnorm(ng, upreg, upregvar)
return(diff)
})
names(diff) <- paste0('group', 1:G)
heatmap(mat, Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
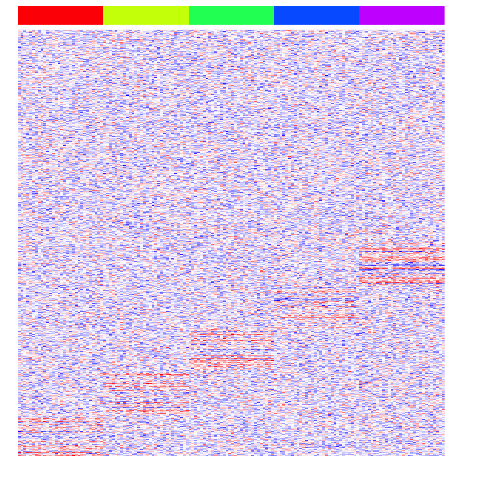
Let’s also simulate some differentially upregulated genes affecting groups of groups. This is typical of cell differentiation processes.
diff2 <- lapply(2:(G-1), function(x) {
y <- x+G
diff <- rownames(mat)[(((y-1)*ng)+1):(((y-1)*ng)+ng)]
mat[diff, group %in% paste0("group", 1:x)] <<- mat[diff, group %in% paste0("group", 1:x)] + rnorm(ng, upreg, upregvar)
return(diff)
})
heatmap(mat, Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
Now, we can begin testing different approaches for multi-group differential expression analysis.
1 vs many (in group vs. not in group)
One approach is to consider each group vs. all others. We can use a simple T-test to test whether each gene is significantly upregulated in each group vs. all other groups.
pv.sig <- lapply(levels(group), function(g){
ingroup <- names(group)[group %in% g]
outgroup <- names(group)[!(group %in% g)]
pv <- sapply(1:M, function(i) {
t.test(mat[i,ingroup], mat[i,outgroup], alternative='greater')$p.value
#t.test(mat[i,ingroup], mat[i,outgroup])$p.value
})
names(pv) <- rownames(mat)
pv.sig <- names(pv)[pv < 0.05/M/G] ## bonferonni
pv.sig
})
heatmap(mat[unique(unlist(pv.sig)),], Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
Indeed, we pick up many of the differentially upregulated genes we simulated that are unique to each group ie. in diff. However, we have a much harder time picking up the differentially upregulated genes marking multiple groups, ie. in diff2 as expected.
perf <- function(pv.sig) {
predtrue <- unique(unlist(pv.sig)) ## predicted differentially expressed genes
predfalse <- setdiff(rownames(mat), predtrue) ## predicted not differentially expressed genes
true <- c(unlist(diff), unlist(diff2)) ## true differentially expressed genes
false <- setdiff(rownames(mat), true) ## true not differentially expressed genes
TP <- sum(predtrue %in% true)
TN <- sum(predfalse %in% false)
FP <- sum(predtrue %in% false)
FN <- sum(predfalse %in% true)
sens <- TP/(TP+FN)
spec <- TN/(TN+FP)
prec <- TP/(TP+FP)
fdr <- FP/(TP+FP)
acc <- (TP+TN)/(TP+FP+FN+TN)
return(data.frame(sens, spec, prec, fdr, acc))
}
print(perf(pv.sig))
## sens spec prec fdr acc
## 1 0.25625 1 1 0 0.405
ANOVA
Alternatively, we can use ANOVA (analysis of variance) to identify genes that are variable among and between groups.
pv <- sapply(1:M, function(i) {
mydataframe <- data.frame(y=mat[i,], ig=group)
fit <- aov(y ~ ig, data=mydataframe)
summary(fit)[[1]][["Pr(>F)"]][1]
})
names(pv) <- rownames(mat)
pv.sig <- names(pv)[pv < 0.05/M/G] ## bonferonni
heatmap(mat[pv.sig,], Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
Note with ANOVA, we need to do an additional step to then figure out which group the variable gene is marking. But compared to testing each group vs. all others, we do get more genes that are differentially upregulated in multiple groups.
print(perf(pv.sig))
## sens spec prec fdr acc
## 1 0.3625 1 1 0 0.49
Testing combined groups (pairs, triplets, etc)
What if we test all possible pairwise combinations of groups?
pv.sig.pair <- lapply(levels(group), function(g1) {
g2 <- setdiff(levels(group), g1)
unlist(lapply(g2, function(g) {
## test two groups vs. all others
ingroup <- names(group)[group %in% c(g1, g)]
outgroup <- names(group)[!(group %in% c(g1, g))]
pv <- sapply(1:M, function(i) {
t.test(mat[i,ingroup], mat[i,outgroup], alternative='greater')$p.value
})
names(pv) <- rownames(mat)
pv.sig <- names(pv)[pv < 0.05/M/G] ## bonferonni
pv.sig
}))
})
heatmap(mat[unique(unlist(pv.sig.pair)),], Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
As expected, we now readily recover the genes upregulated in two groups.
print(perf(pv.sig.pair))
## sens spec prec fdr acc
## 1 0.28125 1 1 0 0.425
Of course, this approach becomes unreasonable if we have many groups. And if we are doing all pairs, why not all triplets. The number of combinations grow exponentially and quickly becomes intractable.
pv.sig.trip <- lapply(levels(group), function(g1) {
g2 <- setdiff(levels(group), g1)
unlist(lapply(g2, function(gi) {
g3 <- setdiff(levels(group), gi)
unlist(lapply(g3, function(gj) {
## test three groups vs. all others
ingroup <- names(group)[group %in% c(g1, gi, gj)]
outgroup <- names(group)[!(group %in% c(g1, gi, gj))]
pv <- sapply(1:M, function(i) {
t.test(mat[i,ingroup], mat[i,outgroup], alternative='greater')$p.value
})
names(pv) <- rownames(mat)
pv.sig <- names(pv)[pv < 0.05/M/G] ## bonferonni
pv.sig
}))
}))
})
heatmap(mat[unique(unlist(pv.sig.trip)),], Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
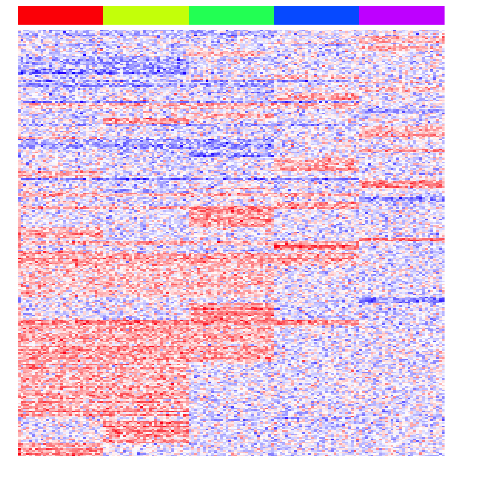
print(perf(pv.sig.trip))
## sens spec prec fdr acc
## 1 0.32625 0.995 0.9961832 0.003816794 0.46
Tree-based binary split
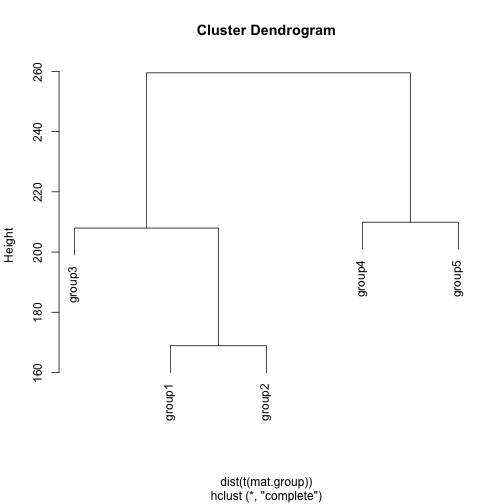
My preferred approach is to assume an underlying tree structure relating groups and compare groups based on recursive binary splits along the tree.
## average gene expression for each group
mat.group <- do.call(cbind, lapply(levels(group), function(g) {
rowMeans(mat[,group==g])
}))
colnames(mat.group) <- levels(group)
## construct tree related groups
hc <- hclust(dist(t(mat.group)), method='complete')
plot(hc)
dend <- as.dendrogram(hc)
pv.sig.all <- c()
pv.recur <- function(dend) {
g1 <- labels(dend[[1]])
g2 <- labels(dend[[2]])
#print(g1)
#print(g2)
ingroup <- names(group)[group %in% g1]
outgroup <- names(group)[group %in% g2]
pv <- sapply(1:M, function(i) {
t.test(mat[i,ingroup], mat[i,outgroup])$p.value
})
names(pv) <- rownames(mat)
pv.sig <- names(pv)[pv < 0.05/M/length(hc$height)] ## bonferonni
#print(pv.sig)
pv.sig.all <<- c(pv.sig.all, pv.sig) ## save
## recursion to go down tree if not leaf
if(!is.leaf(dend[[1]])) {
pv.recur(dend[[1]])
}
if(!is.leaf(dend[[2]])) {
pv.recur(dend[[2]])
}
}
pv.recur(dend)
heatmap(mat[unique(unlist(pv.sig.all)),], Rowv=NA, Colv=NA, col=colorRampPalette(c('blue', 'white', 'red'))(100), scale="none", ColSideColors=rainbow(G)[group], labCol=FALSE, labRow=FALSE)
Of course, the performance of this approach will depend on the initial tree reconstruction.
print(perf(pv.sig.all))
## sens spec prec fdr acc
## 1 0.34 1 1 0 0.472
Conclusion
Try it yourself! What happens if we reduce the degree of upregulation upreg in the simulation? Or increase in variance? What if instead of using a normal, we simulate a zero-inflated negative binomial more characteristic of single cell RNA-seq data? What if we add in different levels of noise to each sample, differential library sizes, and so forth?
RECENT POSTS
- Cross modality image alignment at single cell resolution with STalign on 11 April 2024
- Spatial Transcriptomics Analysis Of Xenium Lymph Node on 24 March 2024
- Querying Google Scholar with Rvest on 18 March 2024
- Alignment of Xenium and Visium spatial transcriptomics data using STalign on 27 December 2023
- Aligning 10X Visium spatial transcriptomics datasets using STalign with Reticulate in R on 05 November 2023
- Aligning single-cell spatial transcriptomics datasets simulated with non-linear disortions on 20 August 2023
- 10x Visium spatial transcriptomics data analysis with STdeconvolve in R on 29 May 2023
- Impact of normalizing spatial transcriptomics data in dimensionality reduction and clustering versus deconvolution analysis with STdeconvolve on 04 May 2023
- Aligning Spatial Transcriptomics Data With Stalign on 16 April 2023
- 3D animation of the brain in R on 08 November 2022