Characterizing spatial heterogeneity using spatial bootstrapping with SEraster
Jul 23, 2024
SEraster aggregates single cell spatial omics data into square/hex pixels for scalable analysis
We recently developed an R package to perform rasterization
preprocessing for spatial omics data called
SEraster. The details of
the framework can be found in our Bioinformatics
paper.
Briefly, SEraster aggregates information in spatial omics data
into non-overlapping, spatial contiguous, square or hexagonal pixels to
speed up and enable other downstream analyses. In our paper, we
demonstrate how SEraster can be applied to effectively speed up
spatial variable gene expression analysis as well as enable the
characterization of cell-type co-enrichment. However, as we have seen
in other blog
posts,
if we can understand the principles underlying a computational method,
we can often apply it to achieve analyses not originally demonstrated.
In this blog post, I will show how I use SEraster to perform spatial
bootstrapping in order to characterize the variability of cell-type
proportions estimates as a function of tissue section size. In
particular, I am interested in characterizing the proportional
representation of cell-types in a tissue However, my cell-type
proportion estimates may be different depending on my tissue section.
But how variable are these estimates? This will depend on aspects of the
tissue such as the “representative-ness” of each section, which will
likely vary depending on the structures inherent in the tissue and the
size of our tissue section. So I will use spatial transcriptomics and
SEraster to evaluate.
Reading in spatial CosMx transcriptomics data
Let’s consider a CosMx SMI Human Liver FFPE spatial transcriptomics dataset from Nanostring (you can download the rather large Seurat object available through the Nanostring website and follow along yourself). Using the gene expression information associated with each cell, the cells have already been clustered and annotated with cell-type names.
Conveniently for me, we already processed this dataset as part of our other paper benchmarking different normalization methods for imaging-based spatial transcriptomics data, so I will simply load in the components I need, which is just the cell-type annotations and cell positions for one tissue section.
## read in data
meta <- readRDS('~/OneDrive - Johns Hopkins/CosMx_liver/data_from_website/cosmx_liver_meta.RDS')
## restrict to one sample of interest
vi <- meta$Run_Tissue_name == 'NormalLiver'
meta <- meta[vi,]
head(meta)
## RNA_pca_cluster_default RNA_pca_cluster_default.1 orig.ident
## c_1_100_10 13 15 c
## c_1_100_1078 7 11 c
## c_1_100_1135 12 10 c
## c_1_100_267 15 17 c
## c_1_100_732 12 10 c
## c_1_100_909 12 19 c
## nCount_RNA nFeature_RNA nCount_negprobes nFeature_negprobes
## c_1_100_10 33 26 0 0
## c_1_100_1078 1699 295 0 0
## c_1_100_1135 173 131 1 1
## c_1_100_267 675 204 2 2
## c_1_100_732 241 167 3 3
## c_1_100_909 300 193 2 2
## nCount_falsecode nFeature_falsecode fov Area AspectRatio Width
## c_1_100_10 5 5 100 2430 1.21 63
## c_1_100_1078 7 7 100 17657 1.80 227
## c_1_100_1135 9 8 100 9382 1.08 121
## c_1_100_267 3 3 100 15449 1.04 166
## c_1_100_732 16 16 100 11206 1.41 145
## c_1_100_909 20 18 100 10987 1.52 188
## Height Mean.PanCK Max.PanCK Mean.CK8.18 Max.CK8.18 Mean.Membrane
## c_1_100_10 52 363 1121 23 274 259
## c_1_100_1078 126 355 1463 1512 6231 384
## c_1_100_1135 112 321 1319 246 3745 699
## c_1_100_267 159 222 907 800 6121 544
## c_1_100_732 103 786 2223 545 2486 1058
## c_1_100_909 124 615 1633 551 5889 903
## Max.Membrane Mean.CD45 Max.CD45 Mean.DAPI Max.DAPI cell_id
## c_1_100_10 911 137 504 457 1508 c_1_100_10
## c_1_100_1078 2110 143 845 3758 16112 c_1_100_1078
## c_1_100_1135 5260 319 3083 3459 14700 c_1_100_1135
## c_1_100_267 3993 61 4755 3710 21732 c_1_100_267
## c_1_100_732 3016 385 3384 4323 20568 c_1_100_732
## c_1_100_909 9566 518 6120 2815 17932 c_1_100_909
## assay_type Run_name slide_ID_numeric Run_Tissue_name Panel
## c_1_100_10 RNA ? 1 NormalLiver 1000plex
## c_1_100_1078 RNA ? 1 NormalLiver 1000plex
## c_1_100_1135 RNA ? 1 NormalLiver 1000plex
## c_1_100_267 RNA ? 1 NormalLiver 1000plex
## c_1_100_732 RNA ? 1 NormalLiver 1000plex
## c_1_100_909 RNA ? 1 NormalLiver 1000plex
## Mean.Yellow Max.Yellow Mean.CD298_B2M Max.CD298_B2M cell_ID
## c_1_100_10 NA NA NA NA c_1_100_10
## c_1_100_1078 NA NA NA NA c_1_100_1078
## c_1_100_1135 NA NA NA NA c_1_100_1135
## c_1_100_267 NA NA NA NA c_1_100_267
## c_1_100_732 NA NA NA NA c_1_100_732
## c_1_100_909 NA NA NA NA c_1_100_909
## x_FOV_px y_FOV_px x_slide_mm y_slide_mm propNegative complexity
## c_1_100_10 2737 25 9.03144 9.73500 0.000000000 1.269231
## c_1_100_1078 595 3998 8.77440 9.25824 0.000000000 5.759322
## c_1_100_1135 1469 4199 8.87928 9.23412 0.005747126 1.320611
## c_1_100_267 3486 1058 9.12132 9.61104 0.002954210 3.308824
## c_1_100_732 3178 2771 9.08436 9.40548 0.012295082 1.443114
## c_1_100_909 3643 3429 9.14016 9.32652 0.006622517 1.554404
## errorCtEstimate percOfDataFromError qcFlagsRNACounts
## c_1_100_10 0 0.0000000 Pass
## c_1_100_1078 0 0.0000000 Pass
## c_1_100_1135 100 0.5780347 Pass
## c_1_100_267 200 0.2962963 Pass
## c_1_100_732 300 1.2448133 Pass
## c_1_100_909 200 0.6666667 Pass
## qcFlagsCellCounts qcFlagsCellPropNeg qcFlagsCellComplex
## c_1_100_10 Pass Pass Pass
## c_1_100_1078 Pass Pass Pass
## c_1_100_1135 Pass Pass Pass
## c_1_100_267 Pass Pass Pass
## c_1_100_732 Pass Pass Pass
## c_1_100_909 Pass Pass Pass
## qcFlagsCellArea median_negprobes negprobes_quantile_0.9 median_RNA
## c_1_100_10 Pass 56 70.7 110
## c_1_100_1078 Pass 56 70.7 110
## c_1_100_1135 Pass 56 70.7 110
## c_1_100_267 Pass 56 70.7 110
## c_1_100_732 Pass 56 70.7 110
## c_1_100_909 Pass 56 70.7 110
## RNA_quantile_0.9 nCell nCount nCountPerCell nFeaturePerCell
## c_1_100_10 690.6 1265 749067 592.1478 145.1549
## c_1_100_1078 690.6 1265 749067 592.1478 145.1549
## c_1_100_1135 690.6 1265 749067 592.1478 145.1549
## c_1_100_267 690.6 1265 749067 592.1478 145.1549
## c_1_100_732 690.6 1265 749067 592.1478 145.1549
## c_1_100_909 690.6 1265 749067 592.1478 145.1549
## propNegativeCellAvg complexityCellAvg errorCtPerCellEstimate
## c_1_100_10 0.001170825 3.644678 45.5336
## c_1_100_1078 0.001170825 3.644678 45.5336
## c_1_100_1135 0.001170825 3.644678 45.5336
## c_1_100_267 0.001170825 3.644678 45.5336
## c_1_100_732 0.001170825 3.644678 45.5336
## c_1_100_909 0.001170825 3.644678 45.5336
## percOfDataFromErrorPerCell qcFlagsFOV cellType
## c_1_100_10 0.07689566 Pass Hep.3
## c_1_100_1078 0.07689566 Pass Hep.4
## c_1_100_1135 0.07689566 Pass Inflammatory.macrophages
## c_1_100_267 0.07689566 Pass Hep.5
## c_1_100_732 0.07689566 Pass Central.venous.LSECs
## c_1_100_909 0.07689566 Pass CD3+.alpha.beta.T.cells
## niche
## c_1_100_10 Zone_3a
## c_1_100_1078 Zone_2a
## c_1_100_1135 Zone_2a
## c_1_100_267 Zone_2a
## c_1_100_732 Zone_2a
## c_1_100_909 Zone_2a
## grab cell-type annotations
ct <- meta$cellType; names(ct) <- rownames(meta)
ct <- as.factor(ct)
head(ct)
## c_1_100_10 c_1_100_1078 c_1_100_1135
## Hep.3 Hep.4 Inflammatory.macrophages
## c_1_100_267 c_1_100_732 c_1_100_909
## Hep.5 Central.venous.LSECs CD3+.alpha.beta.T.cells
## 19 Levels: Antibody.secreting.B.cells ... Stellate.cells
## and positions, convert to um from mm
pos <- meta[, c('x_slide_mm', 'y_slide_mm')] * 1000
colnames(pos) <- c('x', 'y')
head(pos)
## x y
## c_1_100_10 9031.44 9735.00
## c_1_100_1078 8774.40 9258.24
## c_1_100_1135 8879.28 9234.12
## c_1_100_267 9121.32 9611.04
## c_1_100_732 9084.36 9405.48
## c_1_100_909 9140.16 9326.52
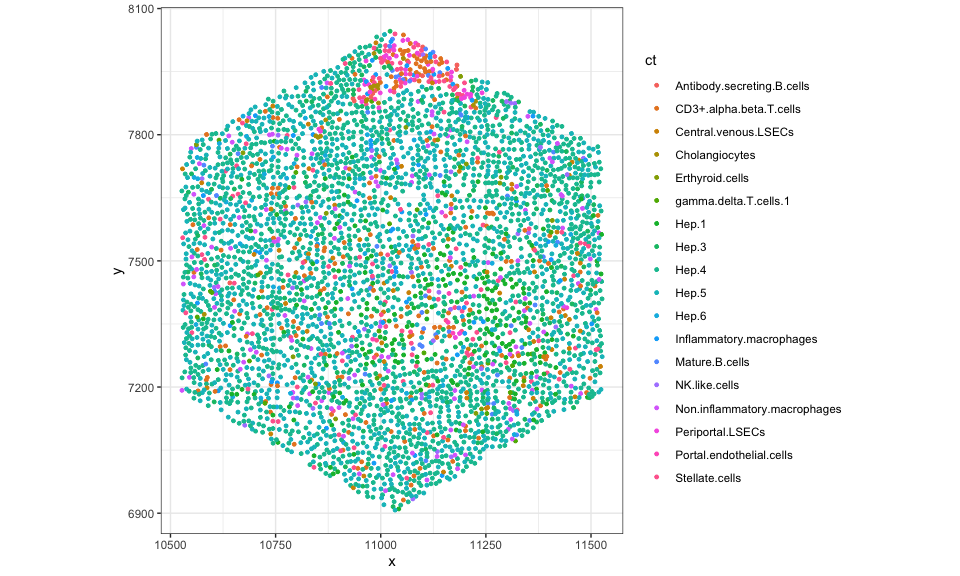
Let’s use ggplot2 to visualize these cell-type annotations in this
tissue section. From this, we can appreciate that this tissue section is
roughly 10mm by 12mm (10000um by 12000um) with ~300k cells comprising
19 cell-types.
length(ct)
## [1] 332877
length(levels(ct))
## [1] 19
## plot
suppressMessages(library(ggplot2))
df <- data.frame(pos, ct = ct)
ggplot(df, aes(x = x, y = y, color = ct)) +
coord_fixed() +
geom_point(size = 0.001) +
theme_bw()
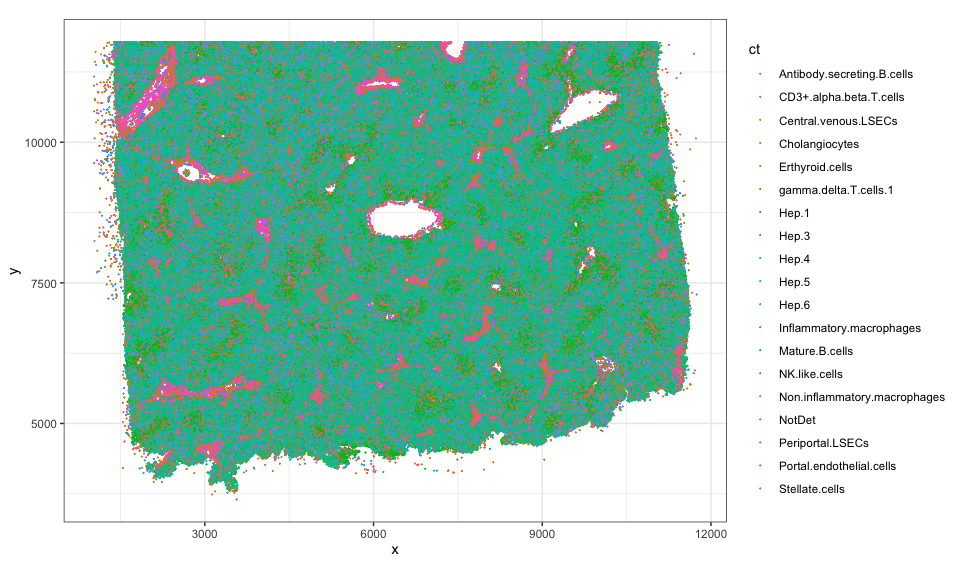If we
estimate the cell-type proportions from this whole tissue, we can
appreciate that roughly 38% of the cells are Hep.4 cells, 5% are
Stellate.cells, 4% are CD3+.alpha.beta.T.cells cells, 2% are
Inflammatory.macrophages and so forth.
## count number of each cell-type, divide by total cells
## and multiply by 100 to make into percents
globalEstimate <- table(ct)/length(ct)*100
sort(globalEstimate)
## ct
## NotDet Portal.endothelial.cells
## 0.001201645 0.161320848
## Erthyroid.cells Antibody.secreting.B.cells
## 0.313629359 0.424481115
## NK.like.cells Mature.B.cells
## 0.826731796 0.879604178
## gamma.delta.T.cells.1 Central.venous.LSECs
## 0.955608228 1.326616137
## Cholangiocytes Inflammatory.macrophages
## 1.436867071 1.767019049
## Periportal.LSECs Hep.6
## 1.827401713 1.857442839
## Non.inflammatory.macrophages CD3+.alpha.beta.T.cells
## 2.870730029 4.104819498
## Stellate.cells Hep.1
## 4.951378437 5.216341171
## Hep.3 Hep.5
## 6.390949209 26.836939771
## Hep.4
## 37.850917907
Using SEraster to create spatial bootstrap samples
However, what if we didn’t have a large 10mm by 12mm tissue section? What if I had a tiny roughly 1mm by 1mm (1000um by 1000um) tissue section? How different would my cell-type proportion estimates be in that case?
Let’s use SEraster to help us find out. I will follow the SEraster
tutorials
to convert my cell positions matrix pos and cell-type annotations
vector ct into a SpatialExperiment object and then use SEraster to
aggregate the cell information into non-overlapping, spatially
contiguous, hexagonal pixels that are 1000um wide. We can plot the
results to appreciate the size of the new hexagonal pixels and the
number of cells per pixel.
suppressMessages(library(SpatialExperiment))
suppressMessages(library(SEraster))
## convert to SE object
spe <- SpatialExperiment::SpatialExperiment(
spatialCoords = as.matrix(pos),
colData = data.frame(ct=ct)
)
## rasterize at 1000um resolution with hexagons
rastCt <- SEraster::rasterizeCellType(spe,
col_name = "ct",
resolution = 1000,
fun = "sum",
square = FALSE)
## plot
SEraster::plotRaster(rastCt, name = "Total Cells")
## Coordinate system already present. Adding new coordinate system, which will
## replace the existing one.
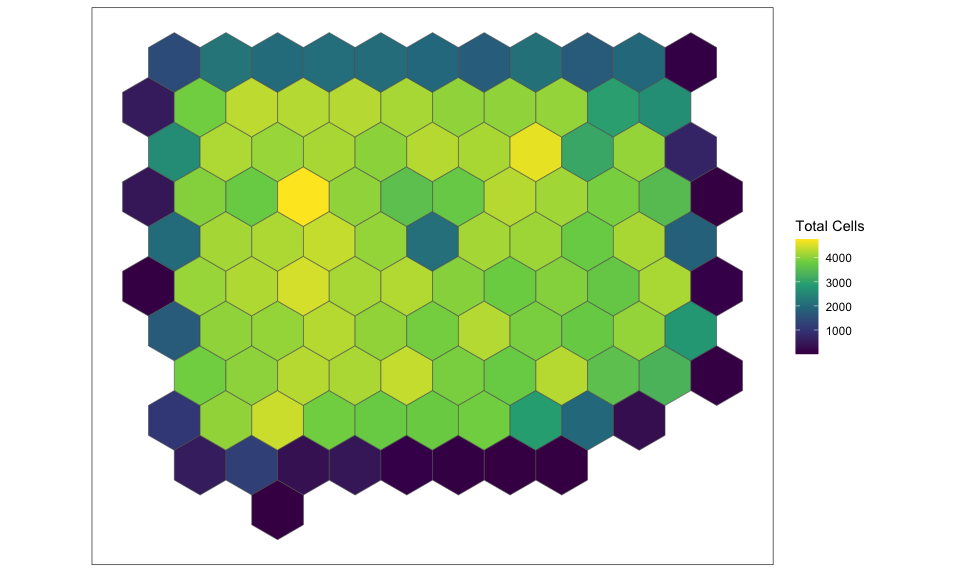
Note that SEraster outputs a SpatialExperiment object. Let’s take a
closer look at the colData slot of this object.
class(rastCt)
## [1] "SpatialExperiment"
## attr(,"package")
## [1] "SpatialExperiment"
head(colData(rastCt))
## DataFrame with 6 rows and 6 columns
## num_cell cellID_list type
## <integer> <list> <character>
## pixel15 30 c_1_169_110,c_1_169_35,c_1_148_40,... hexagon
## pixel16 412 c_1_85_255,c_1_85_93,c_1_106_108,... hexagon
## pixel17 515 c_1_22_152,c_1_22_275,c_1_22_85,... hexagon
## pixel20 1041 c_1_250_650,c_1_250_852,c_1_270_204,... hexagon
## pixel21 1749 c_1_190_370,c_1_190_533,c_1_190_633,... hexagon
## pixel22 2016 c_1_107_810,c_1_107_954,c_1_127_117,... hexagon
## resolution geometry sample_id
## <numeric> <sfc_POLYGON> <character>
## pixel15 1000 list(c(1027, 527, 52.. sample01
## pixel16 1000 list(c(1027, 527, 52.. sample01
## pixel17 1000 list(c(1027, 527, 52.. sample01
## pixel20 1000 list(c(1527, 1027, 1.. sample01
## pixel21 1000 list(c(1527, 1027, 1.. sample01
## pixel22 1000 list(c(1527, 1027, 1.. sample01
We can see that SEraster has kept track of the number of cells in each
of these hexagonal pixels as well as the names of the cells per pixel.
Let’s grab the names of the cells for a few pixels and plot them in the
tissue.
## 20th pixel
cells <- colData(rastCt)$cellID_list[[20]]
## visualize just the cells in this hexagonal pixel
dfsub <- data.frame(pos[cells,], ct = ct[cells])
ggplot(dfsub, aes(x = x, y = y, color = ct)) +
coord_fixed() +
geom_point(size = 1) +
theme_bw()
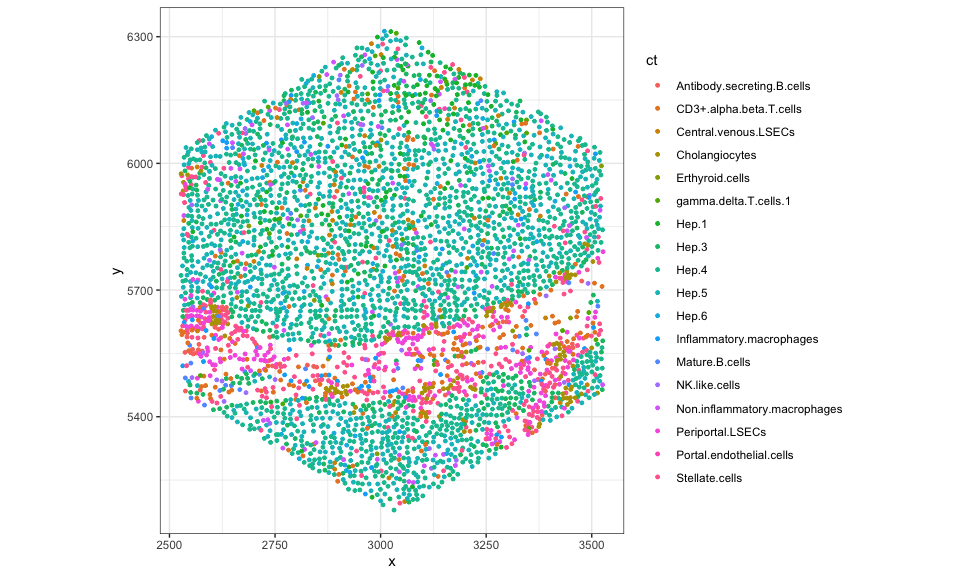
## in whole tissue by setting cells not in hexagonal to NA
ctsub <- ct
ctsub[!(names(ctsub) %in% cells)] <- NA
df <- data.frame(pos, ctsub = ctsub)
ggplot(df, aes(x = x, y = y, color = ctsub)) +
coord_fixed() +
geom_point(size = 0.001) +
theme_bw()
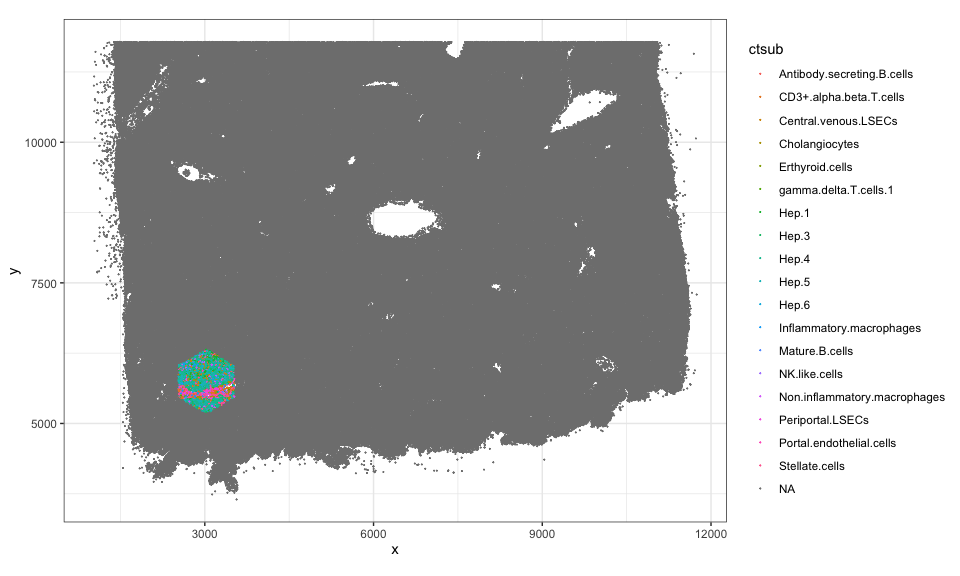
## 100th pixel
cells <- colData(rastCt)$cellID_list[[100]]
## visualize just the cells in this hexagonal pixel
df <- data.frame(pos[cells,], ct = ct[cells])
ggplot(df, aes(x = x, y = y, color = ct)) +
coord_fixed() +
geom_point(size = 1) +
theme_bw()
## in whole tissue by setting cells not in hexagonal to NA
ctsub <- ct
ctsub[!(names(ctsub) %in% cells)] <- NA
df <- data.frame(pos, ctsub = ctsub)
ggplot(df, aes(x = x, y = y, color = ctsub)) +
coord_fixed() +
geom_point(size = 0.001) +
theme_bw()
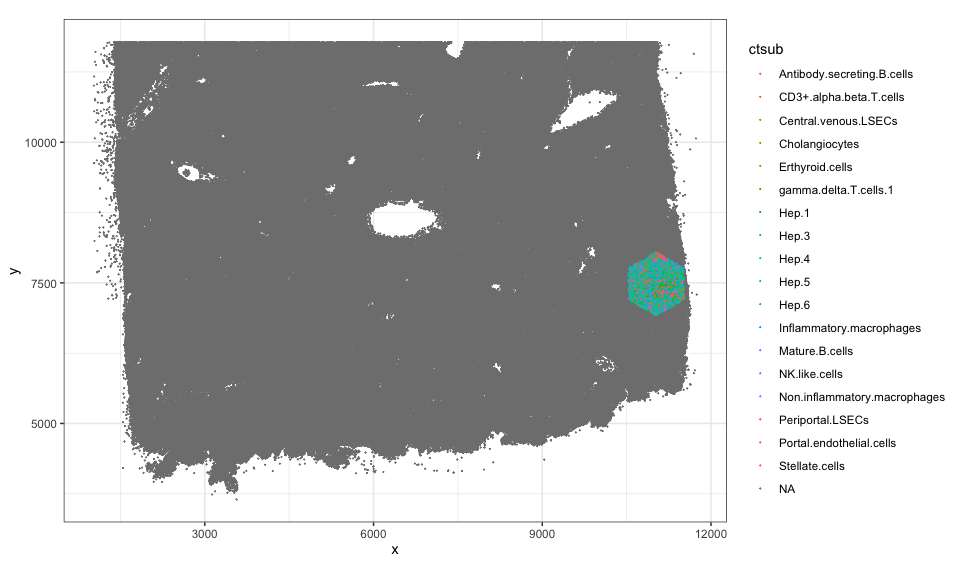
Note we have 109 such pixels.
length(colData(rastCt)$cellID_list)
## [1] 109
Using spatial bootstraps to evaluate stability of cell-type proportions
So let’s see what happens if we estimate the cell-type proportion using just the cells in each hexagonal pixel.
## grab list cell IDs for each hexagonal pixel
cellidsPerBiopsy <- colData(rastCt)$cellID_list
names(cellidsPerBiopsy) <- colnames(rastCt)
## loop through and count number of each cell-type
ctprop <- do.call(rbind, lapply(cellidsPerBiopsy, function(i) {
table(ct[i])
}))
rownames(ctprop) <- names(cellidsPerBiopsy)
head(ctprop)
## Antibody.secreting.B.cells CD3+.alpha.beta.T.cells Central.venous.LSECs
## pixel15 0 17 0
## pixel16 0 34 5
## pixel17 0 48 5
## pixel20 2 58 15
## pixel21 0 64 24
## pixel22 1 114 26
## Cholangiocytes Erthyroid.cells gamma.delta.T.cells.1 Hep.1 Hep.3 Hep.4
## pixel15 0 1 0 0 0 0
## pixel16 9 0 9 4 22 152
## pixel17 3 1 12 4 25 197
## pixel20 29 2 7 154 62 372
## pixel21 22 2 12 233 101 621
## pixel22 3 4 21 107 121 857
## Hep.5 Hep.6 Inflammatory.macrophages Mature.B.cells NK.like.cells
## pixel15 0 0 3 5 4
## pixel16 116 5 6 5 10
## pixel17 152 7 9 14 7
## pixel20 226 6 6 11 9
## pixel21 492 21 17 20 13
## pixel22 525 26 35 21 31
## Non.inflammatory.macrophages NotDet Periportal.LSECs
## pixel15 0 0 0
## pixel16 17 0 4
## pixel17 18 0 0
## pixel20 25 0 5
## pixel21 41 1 1
## pixel22 64 0 3
## Portal.endothelial.cells Stellate.cells
## pixel15 0 0
## pixel16 2 12
## pixel17 0 13
## pixel20 5 47
## pixel21 2 62
## pixel22 3 54
## divide by total cells per pixel
## and multiple by 100 to make into percents
ctpropNorm <- ctprop/rowSums(ctprop)*100
head(rowSums(ctpropNorm)) ## confirm sum is 100
## pixel15 pixel16 pixel17 pixel20 pixel21 pixel22
## 100 100 100 100 100 100
head(ctpropNorm)
## Antibody.secreting.B.cells CD3+.alpha.beta.T.cells Central.venous.LSECs
## pixel15 0.00000000 56.666667 0.0000000
## pixel16 0.00000000 8.252427 1.2135922
## pixel17 0.00000000 9.320388 0.9708738
## pixel20 0.19212296 5.571566 1.4409222
## pixel21 0.00000000 3.659234 1.3722127
## pixel22 0.04960317 5.654762 1.2896825
## Cholangiocytes Erthyroid.cells gamma.delta.T.cells.1 Hep.1
## pixel15 0.0000000 3.3333333 0.0000000 0.0000000
## pixel16 2.1844660 0.0000000 2.1844660 0.9708738
## pixel17 0.5825243 0.1941748 2.3300971 0.7766990
## pixel20 2.7857829 0.1921230 0.6724304 14.7934678
## pixel21 1.2578616 0.1143511 0.6861063 13.3218982
## pixel22 0.1488095 0.1984127 1.0416667 5.3075397
## Hep.3 Hep.4 Hep.5 Hep.6 Inflammatory.macrophages
## pixel15 0.000000 0.00000 0.00000 0.0000000 10.0000000
## pixel16 5.339806 36.89320 28.15534 1.2135922 1.4563107
## pixel17 4.854369 38.25243 29.51456 1.3592233 1.7475728
## pixel20 5.955812 35.73487 21.70989 0.5763689 0.5763689
## pixel21 5.774728 35.50600 28.13036 1.2006861 0.9719840
## pixel22 6.001984 42.50992 26.04167 1.2896825 1.7361111
## Mature.B.cells NK.like.cells Non.inflammatory.macrophages NotDet
## pixel15 16.666667 13.3333333 0.000000 0.00000000
## pixel16 1.213592 2.4271845 4.126214 0.00000000
## pixel17 2.718447 1.3592233 3.495146 0.00000000
## pixel20 1.056676 0.8645533 2.401537 0.00000000
## pixel21 1.143511 0.7432819 2.344197 0.05717553
## pixel22 1.041667 1.5376984 3.174603 0.00000000
## Periportal.LSECs Portal.endothelial.cells Stellate.cells
## pixel15 0.00000000 0.0000000 0.000000
## pixel16 0.97087379 0.4854369 2.912621
## pixel17 0.00000000 0.0000000 2.524272
## pixel20 0.48030740 0.4803074 4.514890
## pixel21 0.05717553 0.1143511 3.544883
## pixel22 0.14880952 0.1488095 2.678571
And let’s visualize the resulting cell-type proportions per hexagonal pixel as a stacked barplot.
suppressMessages(library(reshape2))
# Melt the data frame to long format
df <- data.frame(ctpropNorm)
df$Sample <- rownames(df)
dfLong <- melt(df, id.vars = "Sample", variable.name = "CellType", value.name = "Proportion")
head(dfLong)
## Sample CellType Proportion
## 1 pixel15 Antibody.secreting.B.cells 0.00000000
## 2 pixel16 Antibody.secreting.B.cells 0.00000000
## 3 pixel17 Antibody.secreting.B.cells 0.00000000
## 4 pixel20 Antibody.secreting.B.cells 0.19212296
## 5 pixel21 Antibody.secreting.B.cells 0.00000000
## 6 pixel22 Antibody.secreting.B.cells 0.04960317
# Create the stacked barplot using ggplot2
ggplot(dfLong, aes(x = Sample, y = Proportion, fill = CellType)) +
geom_bar(stat = "identity") +
labs(title = "Stacked Barplot of Cell Type Proportions",
x = "Sample",
y = "Proportion") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1, size=5))
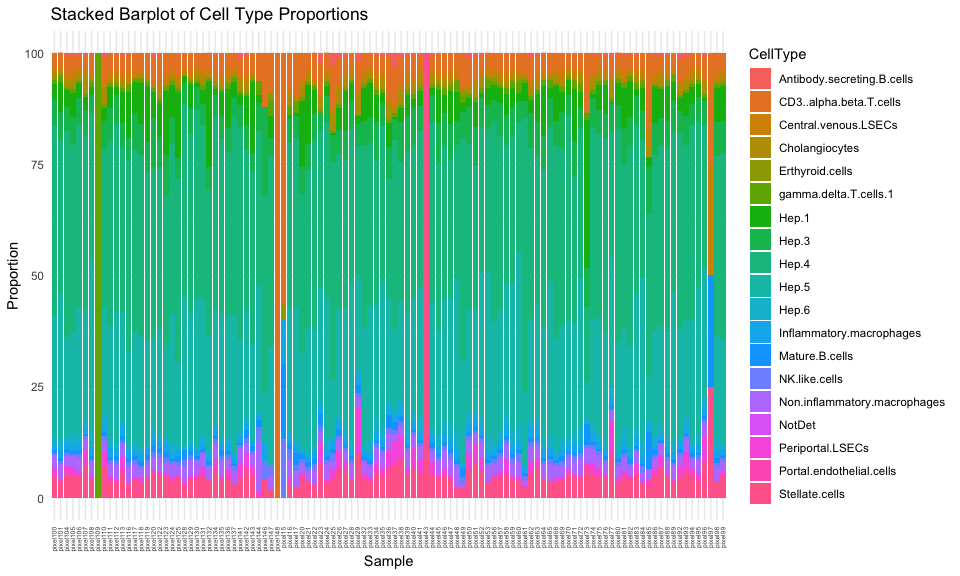
There are definitely some hexagonal pixels that have very distinct cell-type proportions. Let’s see which ones are the most different from our global cell-type proportion estimate.
diff <- sapply(1:nrow(ctpropNorm), function(i) {
sum((ctpropNorm[i,]-globalEstimate)^2)
})
names(diff) <- rownames(ctpropNorm)
head(sort(diff, decreasing=TRUE))
## pixel109 pixel148 pixel43 pixel15 pixel97 pixel73
## 12095.864 11466.022 11296.710 5510.753 4223.865 1688.273
Indeed, it looks like our estimate of cell-type proportions is quite
different for this pixel109 compared to original global estimate. In
pixel109, 100% of the cells are of the gamma.delta.T.cells.1
cell-type! However, if we look closer, it seems like this hexagonal
pixel only has 1 cell in it!
ctpropNorm['pixel109',]
## Antibody.secreting.B.cells CD3+.alpha.beta.T.cells
## 0 0
## Central.venous.LSECs Cholangiocytes
## 0 0
## Erthyroid.cells gamma.delta.T.cells.1
## 0 100
## Hep.1 Hep.3
## 0 0
## Hep.4 Hep.5
## 0 0
## Hep.6 Inflammatory.macrophages
## 0 0
## Mature.B.cells NK.like.cells
## 0 0
## Non.inflammatory.macrophages NotDet
## 0 0
## Periportal.LSECs Portal.endothelial.cells
## 0 0
## Stellate.cells
## 0
colData(rastCt)['pixel109',]
## DataFrame with 1 row and 6 columns
## num_cell cellID_list type resolution geometry
## <integer> <list> <character> <numeric> <sfc_POLYGON>
## pixel109 1 c_1_301_25 hexagon 1000 list(c(9027, 8527, 8..
## sample_id
## <character>
## pixel109 sample01
## plot pixel109
cells <- colData(rastCt)$cellID_list[[109]]
## visualize just the cells in this hexagonal pixel
df <- data.frame(pos[cells,], ct = ct[cells])
ggplot(df, aes(x = x, y = y, color = ct)) +
coord_fixed() +
geom_point(size = 1) +
theme_bw()
## in whole tissue by setting cells not in hexagonal to NA
ctsub <- ct
ctsub[!(names(ctsub) %in% cells)] <- NA
df <- data.frame(pos, ctsub = ctsub)
ggplot(df, aes(x = x, y = y, color = ctsub)) +
coord_fixed() +
geom_point(size = 0.001) +
theme_bw()
If we look at the total number of cells per hexagonal pixel versus how different their cell-type proportion estimate is from the global estimate, we definitely see an association where pixels with very few cells are more different in their estimates as expected. These pixels are likely towards the edge of the tissue and therefore not very representative.
df <- data.frame(num_cell = colData(rastCt)$num_cell, diff = diff)
## note we are plotting on a log scale!
ggplot(df, aes(x=num_cell, y=diff)) + geom_point() + scale_x_log10() + scale_y_log10()
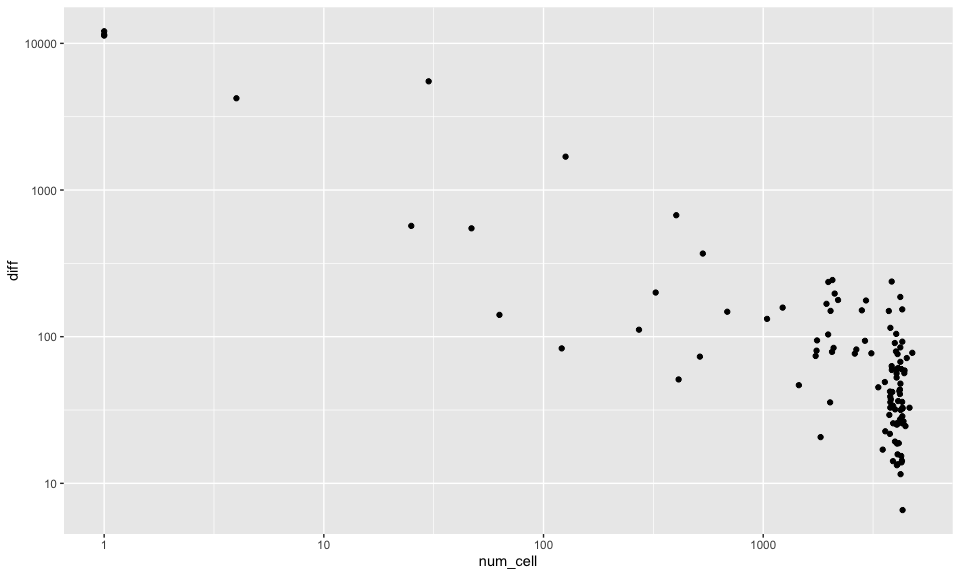
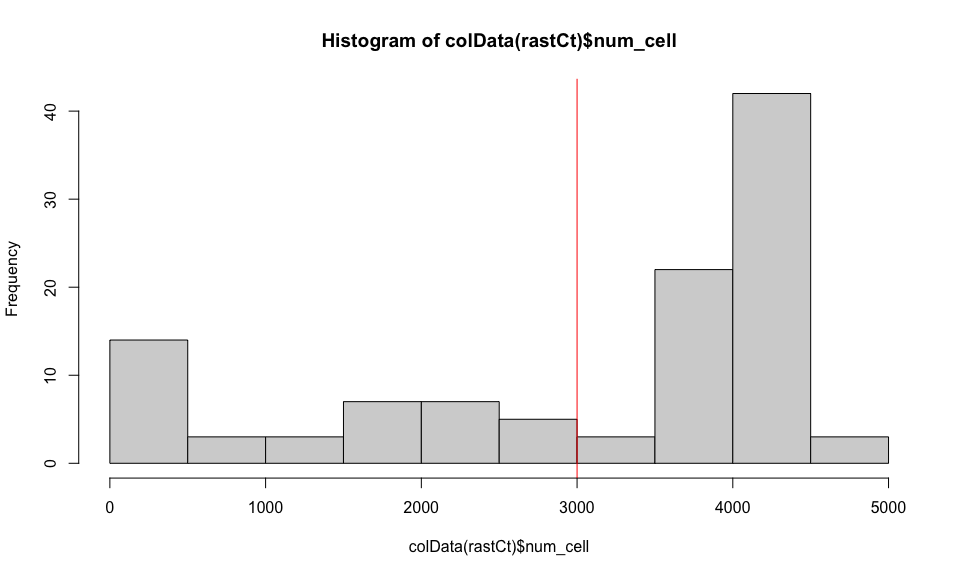
If we restrict to hexagonal pixels with more than 3000 cells, we can confirm these pixels are not on the edge of the tissue section.
## histogram of number of cells per pixel
hist(colData(rastCt)$num_cell)
abline(v = 3000, col='red')
## get pixels with more than 3000 cells
goodPixels <- colnames(rastCt)[colData(rastCt)$num_cell > 3000]
length(goodPixels)
## [1] 70
head(goodPixels)
## [1] "pixel26" "pixel27" "pixel28" "pixel29" "pixel32" "pixel33"
SEraster::plotRaster(rastCt[, goodPixels], name = "Total Cells")
## Coordinate system already present. Adding new coordinate system, which will
## replace the existing one.
And now, we can see a pretty consistent cell-type proportion distribution compared to our original global estimate.
## just look at ctpropNorm for good pixels
df <- data.frame(ctpropNorm[goodPixels,])
df$Sample <- rownames(df)
dfLong <- melt(df, id.vars = "Sample", variable.name = "CellType", value.name = "Proportion")
ggplot(dfLong, aes(x = Sample, y = Proportion, fill = CellType)) +
geom_bar(stat = "identity") +
labs(title = "Stacked Barplot of Cell Type Proportions",
x = "Sample",
y = "Proportion") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1, size=5))
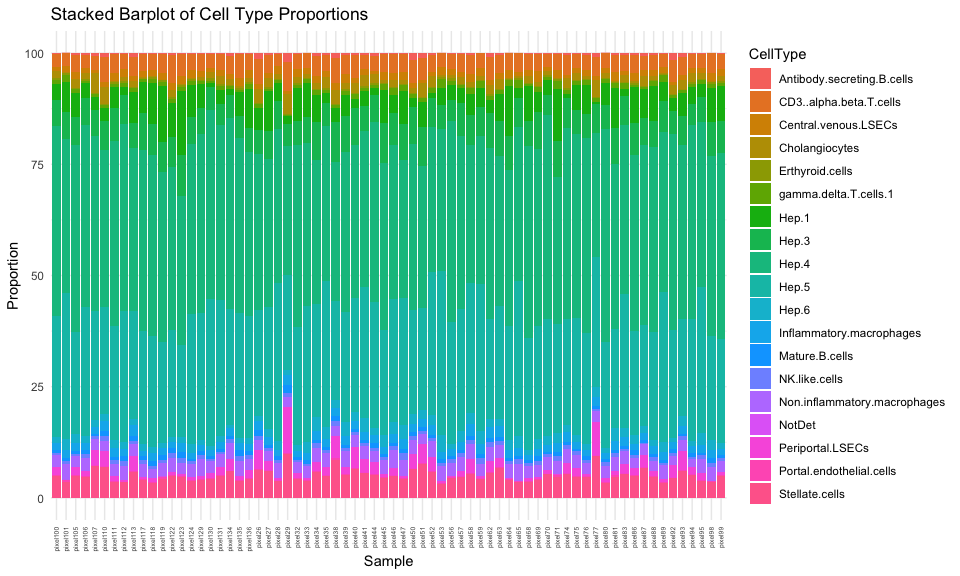
We can even focus on just one cell-type, for example the
Stellate.cells, and fit a gaussian distribution to all the estimates
of this cell-type’s proportional representation across all of our
hexagonal pixels.
cct <- 'Stellate.cells'
cellProportions <- ctpropNorm[goodPixels,cct]
df <- data.frame(x = cellProportions)
# Fit Gaussian distribution
mu <- mean(cellProportions)
sigma <- sd(cellProportions)
x <- seq(0, 25, length.out = 100) # fit from 0 to 25%
y <- dnorm(x, mean = mu, sd = sigma)
fit <- data.frame(x = x, y = y)
# Add Gaussian distribution line to the plot
ggplot(df, aes(x = x)) +
geom_histogram(binwidth = 0.02, color = "black") +
labs(title = paste0("Estimate of ", cct, " Cell-Type Proportion\nin the Liver from 100um Hexagonal Pixels"),
x = paste0(cct, " Cell-Type Proportion"),
y = "Frequency") +
theme_minimal() +
geom_line(data = fit, aes(x = x, y = y), color = "red", linewidth = 1)
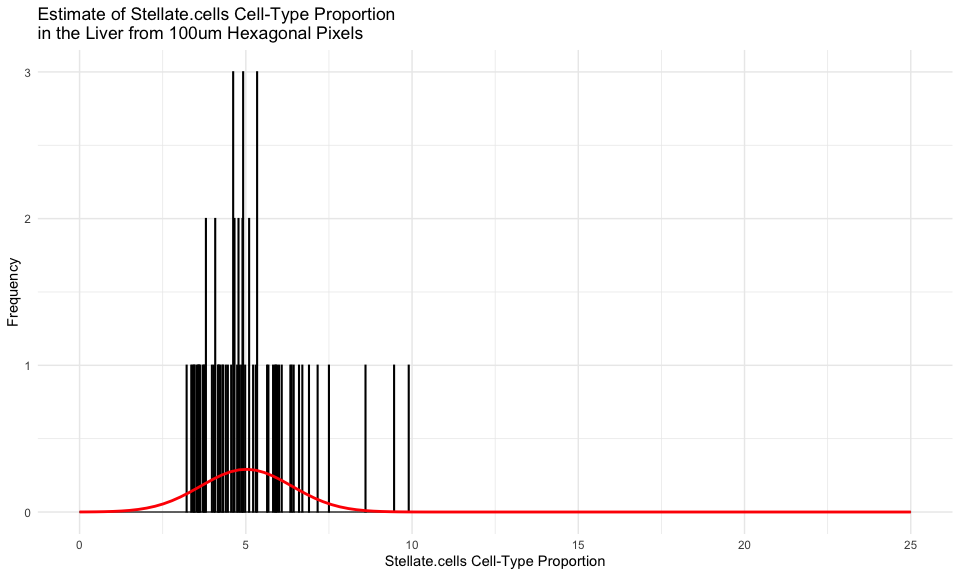
According to Wikipedia, which cites this paper, “in normal liver…stellate cells represent 5-8% of the total number of liver cells.” So it seems like our estimate is pretty consistent!
Of course while this type of spatial bootstrapping does not account for inter-patient variability or other technical and biological variation that may contribute to cell-type proportion variability, it can give us a sense for the degree of intra-sample cell-type proportion variability for tissue sections of a particular size, in this case 1000um.
Try it out for yourself!
- If you choose a square pixel instead of hexagonal by setting
square = TRUE, how do the results change? - If you choose a smaller (or larger) hexagonal pixel size, how do the results change?
- Calculate another statistic per pixel such as cell-type spatial colocalization relationships and evaluate its stability.
- Apply what you’ve learned towards your own spatial omics data analysis.
RECENT POSTS
- Using AI to find heterogeneous scientific speakers on 04 November 2024
- The many ways to calculate Moran's I for identifying spatially variable genes in spatial transcriptomics data on 29 August 2024
- Characterizing spatial heterogeneity using spatial bootstrapping with SEraster on 23 July 2024
- I use R to (try to) figure out which hospital I should go to for shoppable medical services by comparing costs through analyzing Hospital Price Transparency data on 22 April 2024
- Cross modality image alignment at single cell resolution with STalign on 11 April 2024
- Spatial Transcriptomics Analysis Of Xenium Lymph Node on 24 March 2024
- Querying Google Scholar with Rvest on 18 March 2024
- Alignment of Xenium and Visium spatial transcriptomics data using STalign on 27 December 2023
- Aligning 10X Visium spatial transcriptomics datasets using STalign with Reticulate in R on 05 November 2023
- Aligning single-cell spatial transcriptomics datasets simulated with non-linear disortions on 20 August 2023
TAGS
RELATED POSTS
- Using AI to find heterogeneous scientific speakers
- The many ways to calculate Moran's I for identifying spatially variable genes in spatial transcriptomics data
- I use R to (try to) figure out which hospital I should go to for shoppable medical services by comparing costs through analyzing Hospital Price Transparency data
- Cross modality image alignment at single cell resolution with STalign