Aligning heart ST data from ISS
Serial sections of 6.5 PCW human heart from the Human Cell Atlas https://doi.org/10.1016/j.cell.2019.11.025
[1]:
# import dependencies
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import torch
# make plots bigger
plt.rcParams["figure.figsize"] = (12,10)
[ ]:
# OPTION A: import STalign after pip or pipenv install
from STalign import STalign
[2]:
## OPTION B: skip cell if installed STalign with pip or pipenv
import sys
sys.path.append("../../STalign")
## import STalign from upper directory
import STalign
We have already downloaded single cell spatial transcriptomics datasets and placed the files in a folder called data_data.
We can read in the cell information for the first dataset using pandas as pd.
[3]:
# Single cell data 1
# read in data
fname = '../heart_data/CN73_E1.csv.gz'
df1 = pd.read_csv(fname)
print(df1.head())
Unnamed: 0 x y intensity area id color \
0 1 9220.548828 27954.275391 126.357140 34 NaN #000000
1 2 16412.062500 27723.751953 170.324326 86 NaN #000000
2 3 16451.130859 27567.246094 170.600006 46 NaN #000000
3 4 18739.607422 27238.117188 170.125000 34 NaN #000000
4 5 18713.855469 27219.013672 171.300003 46 NaN #000000
acronym right.left rostral.caudal spot.id image
0 NaN -58.104428 775.168105 NaN CN73_E1
1 NaN 127.199485 775.176714 NaN CN73_E1
2 NaN 132.844121 775.176714 NaN CN73_E1
3 NaN 216.521727 775.176714 NaN CN73_E1
4 NaN 216.521080 775.176714 NaN CN73_E1
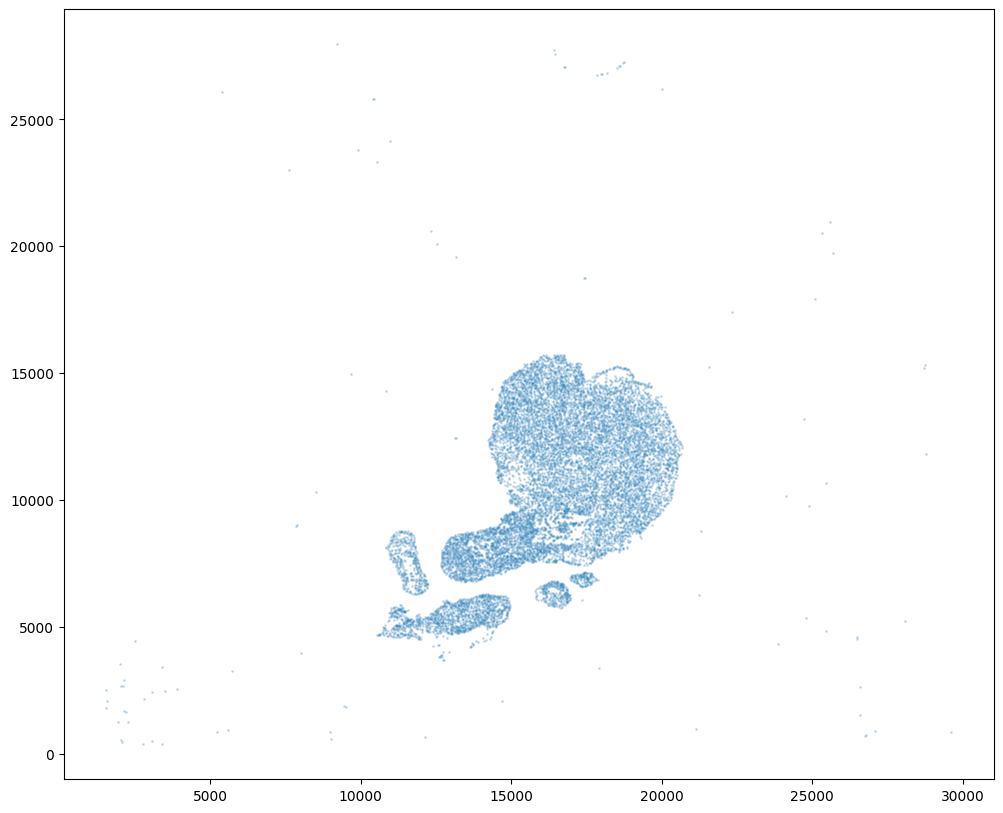
For alignment with STalign, we only need the cell centroid information. So we can pull out this information. We can further visualize the cell centroids to get a sense of the variation in cell density that we will be relying on for our alignment by plotting using matplotlib.pyplot as plt.
[4]:
# get cell centroid coordinates
xI = np.array(df1['x'])
yI = np.array(df1['y'])
# plot
fig,ax = plt.subplots()
ax.scatter(xI,yI,s=1,alpha=0.2)
[4]:
<matplotlib.collections.PathCollection at 0x7f2ad9a0d7f0>
We will first use STalign to rasterize the single cell centroid positions into an image. Assuming the single-cell centroid coordinates are in microns, we will perform this rasterization at a 100 micron resolution. We can visualize the resulting rasterized image.
Note that points are plotting with the origin at bottom left while images are typically plotted with origin at top left so we’ve used invert_yaxis() to invert the yaxis for visualization consistency.
[5]:
# rasterize at 100um resolution so image looks smooth
XI,YI,I,fig = STalign.rasterize(xI,yI,dx=100)
# plot
ax = fig.axes[0]
ax.invert_yaxis()
0 of 12183
10000 of 12183
12182 of 12183

Now, we can repeat this for the cell information from the second dataset.
[6]:
# Single cell data 2
# read in data
fname = '../heart_data/CN73_E2.csv.gz'
df2 = pd.read_csv(fname, skiprows=[1]) # first row is data type
print(df2.head())
Unnamed: 0 x y intensity area id color \
0 12185 3965.500000 26604.583984 178.437500 32 NaN #000000
1 12186 902.051270 26600.513672 151.615387 26 NaN #000000
2 12187 3949.748047 26560.296875 156.199997 90 NaN #000000
3 12188 6231.878906 26551.273438 152.812500 22 NaN #000000
4 12189 12881.071289 26510.095703 197.307693 112 NaN #000000
acronym right.left rostral.caudal spot.id image
0 NaN -459.896378 1097.377561 NaN CN73_E2
1 NaN -643.887328 1104.877930 NaN CN73_E2
2 NaN -461.396305 1094.377414 NaN CN73_E2
3 NaN -324.403043 1089.877192 31.0 CN73_E2
4 NaN 95.076323 1098.877635 10.0 CN73_E2
[7]:
# get cell centroids
xJ = np.array(df2['x'])
yJ = np.array(df2['y'])
# plot
fig,ax = plt.subplots()
ax.scatter(xJ,yJ,s=1,alpha=0.2,c='#ff7f0e')
[7]:
<matplotlib.collections.PathCollection at 0x7f2ad996c490>
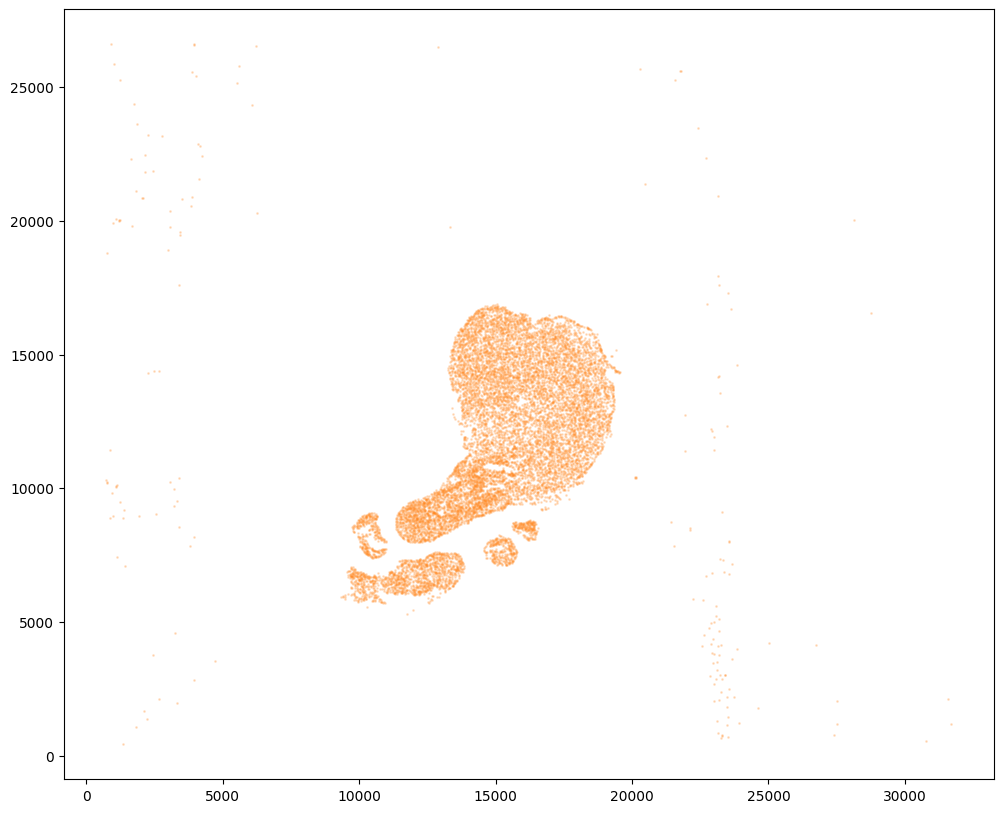
[8]:
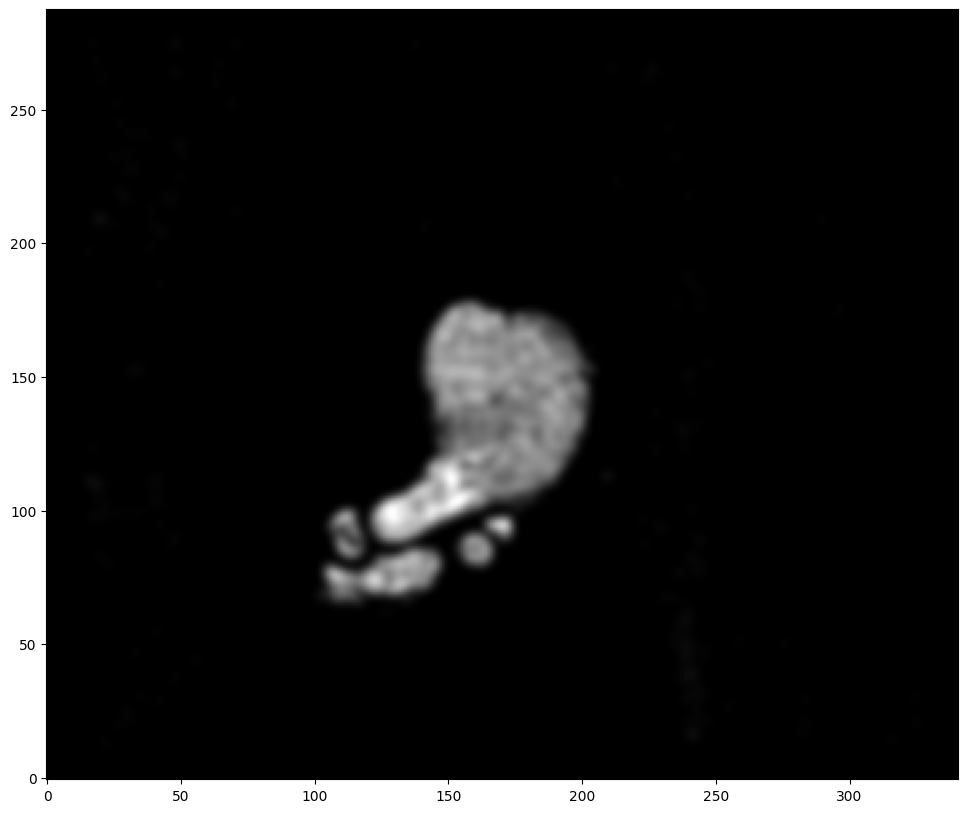
# rasterize and plot
XJ,YJ,J,fig = STalign.rasterize(xJ,yJ,dx=100)
ax = fig.axes[0]
ax.invert_yaxis()
0 of 11770
10000 of 11770
11769 of 11770
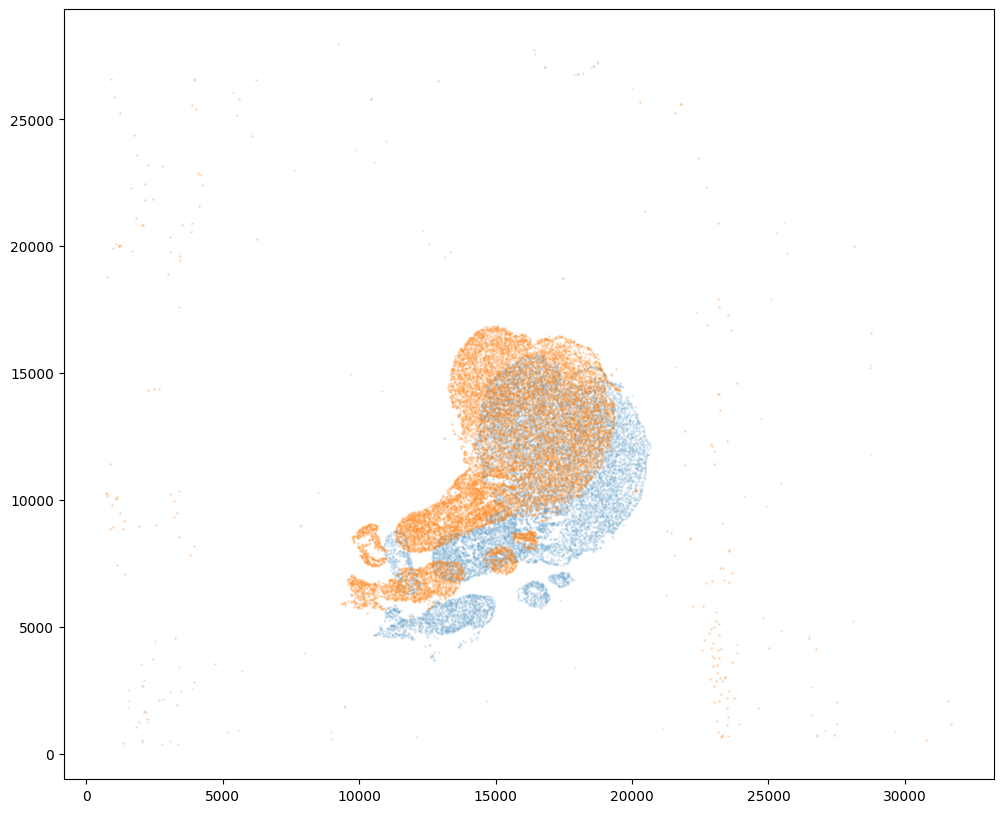
Note that plotting the cell centroid positions from both datasets shows that non-linear local alignment is needed.
[9]:
# plot
fig,ax = plt.subplots()
ax.scatter(xI,yI,s=1,alpha=0.1)
ax.scatter(xJ,yJ,s=1,alpha=0.2)
[9]:
<matplotlib.collections.PathCollection at 0x7f2ad9863ca0>
We can also plot the rasterized images next to each other.
[10]:
# get extent of images
extentI = STalign.extent_from_x((YI,XI))
extentJ = STalign.extent_from_x((YJ,XJ))
# plot rasterized images
fig,ax = plt.subplots(2,1)
ax[0].imshow((I.transpose(1,2,0).squeeze()), extent=extentI)
ax[1].imshow((J.transpose(1,2,0).squeeze()), extent=extentJ)
ax[0].invert_yaxis()
ax[1].invert_yaxis()
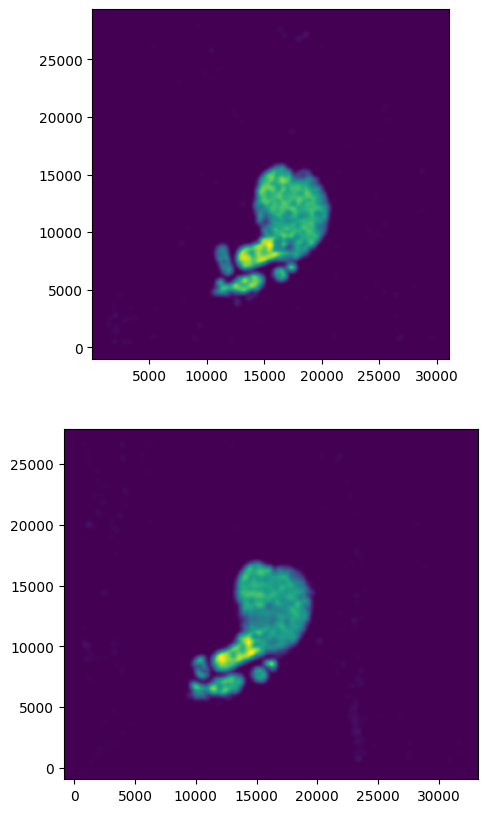
Now we will perform our alignment. There are many parameters that can be tuned for performing this alignment. If we don’t specify parameters, defaults will be used.
[11]:
# set device for building tensors
if torch.cuda.is_available():
torch.set_default_device('cuda:0')
else:
torch.set_default_device('cpu')
[12]:
%%time
# run LDDMM
# specify device (default device for STalign.LDDMM is cpu)
if torch.cuda.is_available():
device = 'cuda:0'
else:
device = 'cpu'
# keep all other parameters default
params = {
'niter':1000,
'device':device,
'diffeo_start':100,
'a':250,
'epV':1000,
'sigmaB':0.1,
'muB': torch.tensor([0,0,0]), # black is background in target
}
Ifoo = np.vstack((I, I, I)) # make RGB instead of greyscale
Jfoo = np.vstack((J, J, J)) # make RGB instead of greyscale
out = STalign.LDDMM([YI,XI],Ifoo,[YJ,XJ],Jfoo,**params)
/home/kalen/.local/share/virtualenvs/STalign-VWNsoi3D/lib/python3.8/site-packages/torch/utils/_device.py:62: UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.clone().detach() or sourceTensor.clone().detach().requires_grad_(True), rather than torch.tensor(sourceTensor).
return func(*args, **kwargs)
/home/kalen/.local/share/virtualenvs/STalign-VWNsoi3D/lib/python3.8/site-packages/torch/functional.py:504: UserWarning: torch.meshgrid: in an upcoming release, it will be required to pass the indexing argument. (Triggered internally at ../aten/src/ATen/native/TensorShape.cpp:3483.)
return _VF.meshgrid(tensors, **kwargs) # type: ignore[attr-defined]
/home/kalen/STalign/docs/notebooks/../../STalign/STalign.py:1301: UserWarning: Data has no positive values, and therefore cannot be log-scaled.
axE[2].set_yscale('log')
/home/kalen/.local/share/virtualenvs/STalign-VWNsoi3D/lib/python3.8/site-packages/matplotlib/cm.py:478: RuntimeWarning: invalid value encountered in cast
xx = (xx * 255).astype(np.uint8)
CPU times: user 3min 42s, sys: 35 s, total: 4min 17s
Wall time: 2min 4s
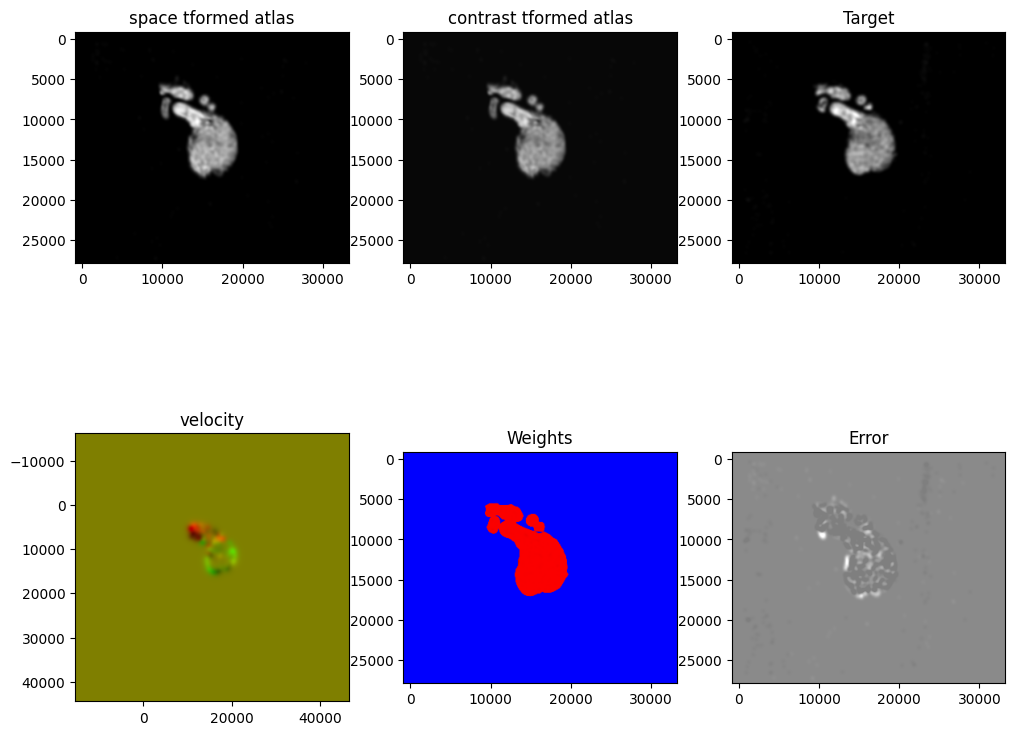
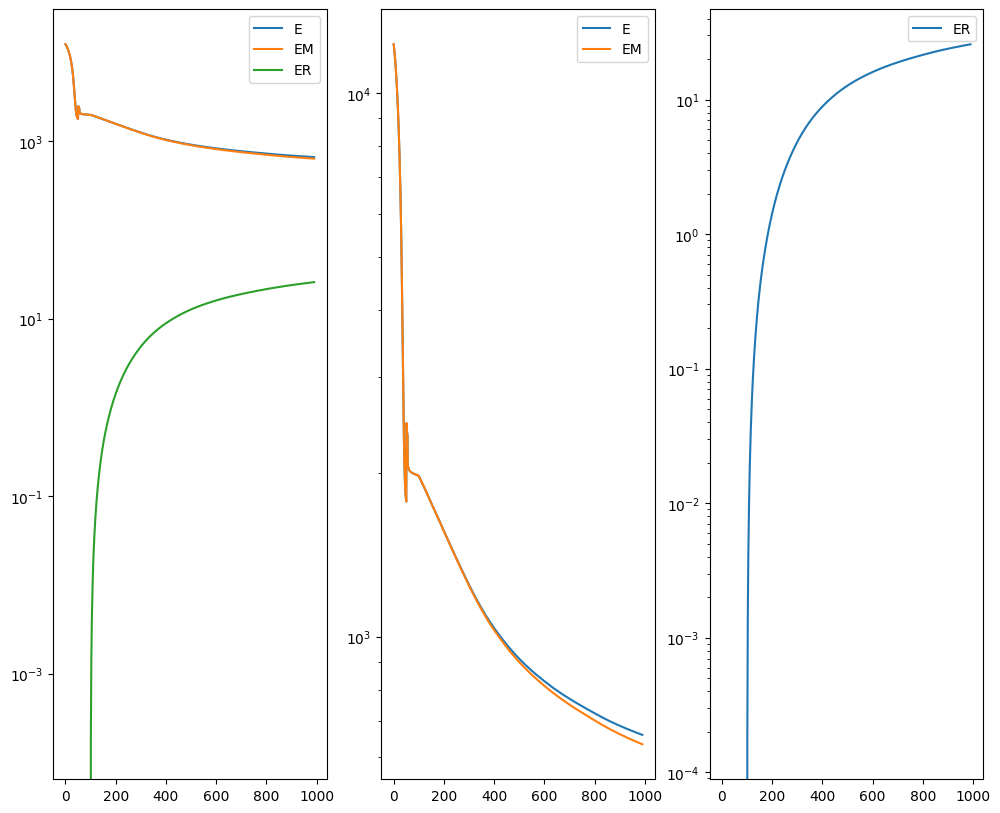
[13]:
# get necessary output variables
A = out['A']
v = out['v']
xv = out['xv']
Plots generated throughout the alignment can be used to give you a sense of whether the parameter choices are appropriate and whether your alignment is converging on a solution.
We can also evaluate the resulting alignment by applying the transformation to visualize how our source and target images were deformed to achieve the alignment.
[14]:
# apply transform
phii = STalign.build_transform(xv,v,A,XJ=[YJ,XJ],direction='b')
phiI = STalign.transform_image_source_to_target(xv,v,A,[YI,XI],Ifoo,[YJ,XJ])
#switch tensor from cuda to cpu for plotting with numpy
if phii.is_cuda:
phii = phii.cpu()
if phiI.is_cuda:
phiI = phiI.cpu()
# plot with grids
fig,ax = plt.subplots()
levels = np.arange(-100000,100000,1000)
ax.contour(XJ,YJ,phii[...,0],colors='r',linestyles='-',levels=levels)
ax.contour(XJ,YJ,phii[...,1],colors='g',linestyles='-',levels=levels)
ax.set_aspect('equal')
ax.set_title('source to target')
ax.imshow(phiI.permute(1,2,0)/torch.max(phiI),extent=extentJ)
ax.invert_yaxis()
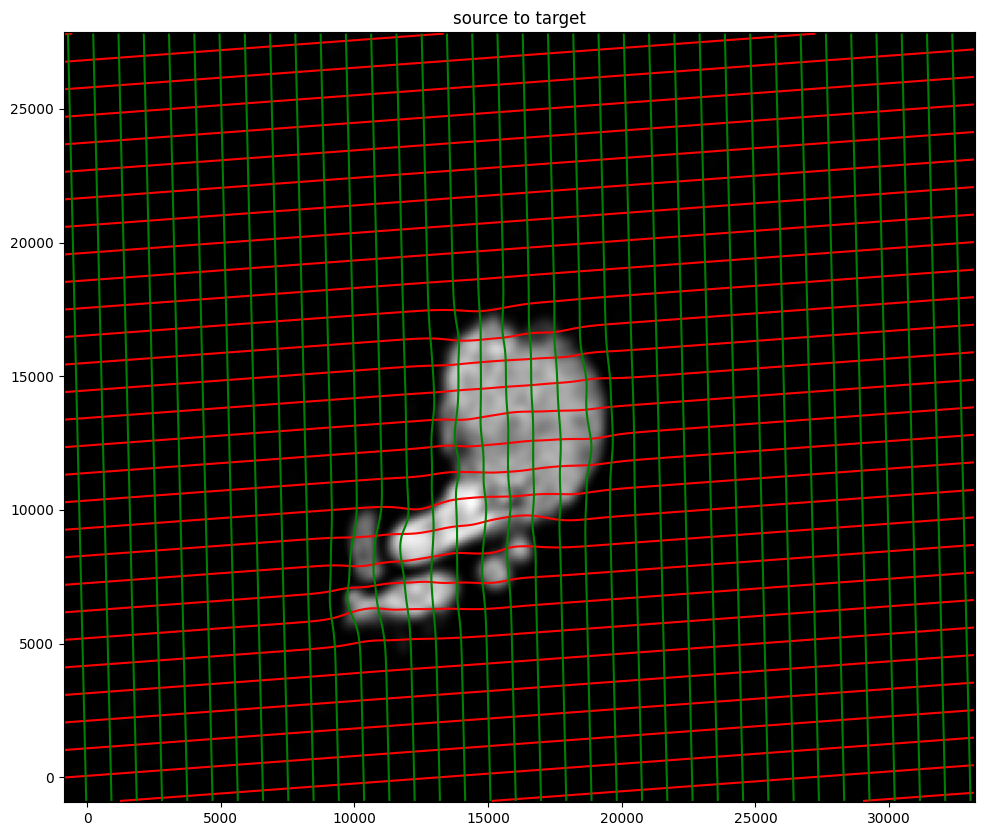
Note that because of our use of LDDMM, the resulting transformation is invertible.
[15]:
# transform is invertible
phi = STalign.build_transform(xv,v,A,XJ=[YI,XI],direction='f')
phiiJ = STalign.transform_image_target_to_source(xv,v,A,[YJ,XJ],Jfoo,[YI,XI])
#switch tensor from cuda to cpu for plotting with numpy
if phi.is_cuda:
phi = phi.cpu()
if phiiJ.is_cuda:
phiiJ = phiiJ.cpu()
# plot with grids
fig,ax = plt.subplots()
levels = np.arange(-100000,100000,1000)
ax.contour(XI,YI,phi[...,0],colors='r',linestyles='-',levels=levels)
ax.contour(XI,YI,phi[...,1],colors='g',linestyles='-',levels=levels)
ax.set_aspect('equal')
ax.set_title('target to source')
ax.imshow(phiiJ.permute(1,2,0)/torch.max(phiiJ),extent=extentI)
ax.invert_yaxis()
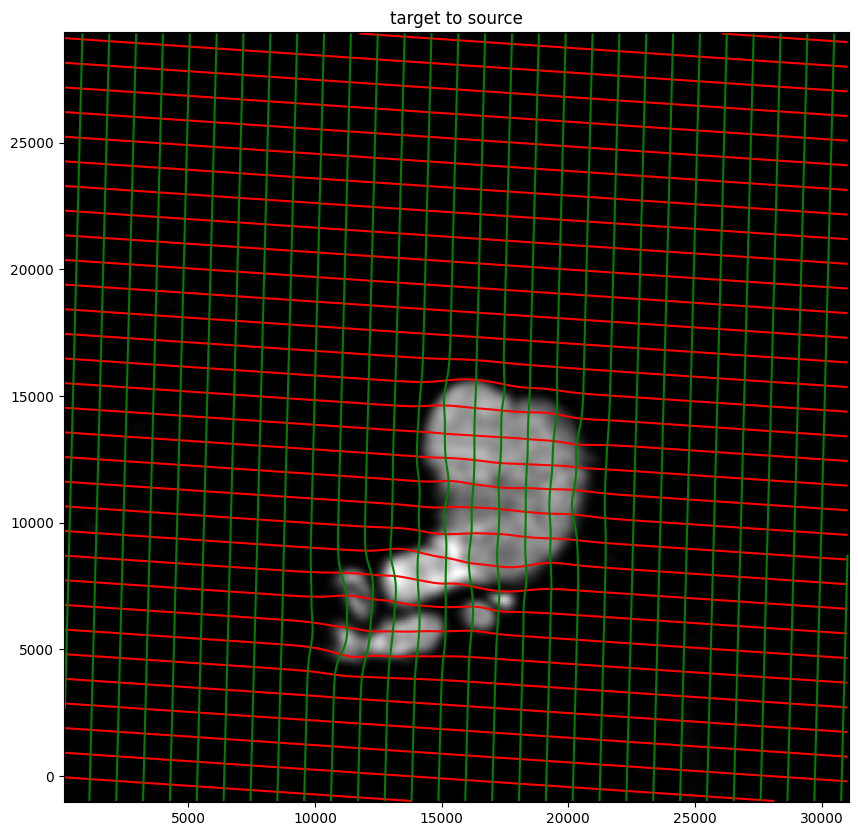
Finally, we can apply our transform to the original sets of single cell centroid positions to achieve their new aligned positions.
[16]:
# apply transform to original points
tpointsJ = STalign.transform_points_target_to_source(xv,v,A, np.stack([yJ, xJ], 1))
#switch tensor from cuda to cpu for plotting with numpy
if tpointsJ.is_cuda:
tpointsJ = tpointsJ.cpu()
# just original points for visualizing later
tpointsI = np.stack([xI, yI])
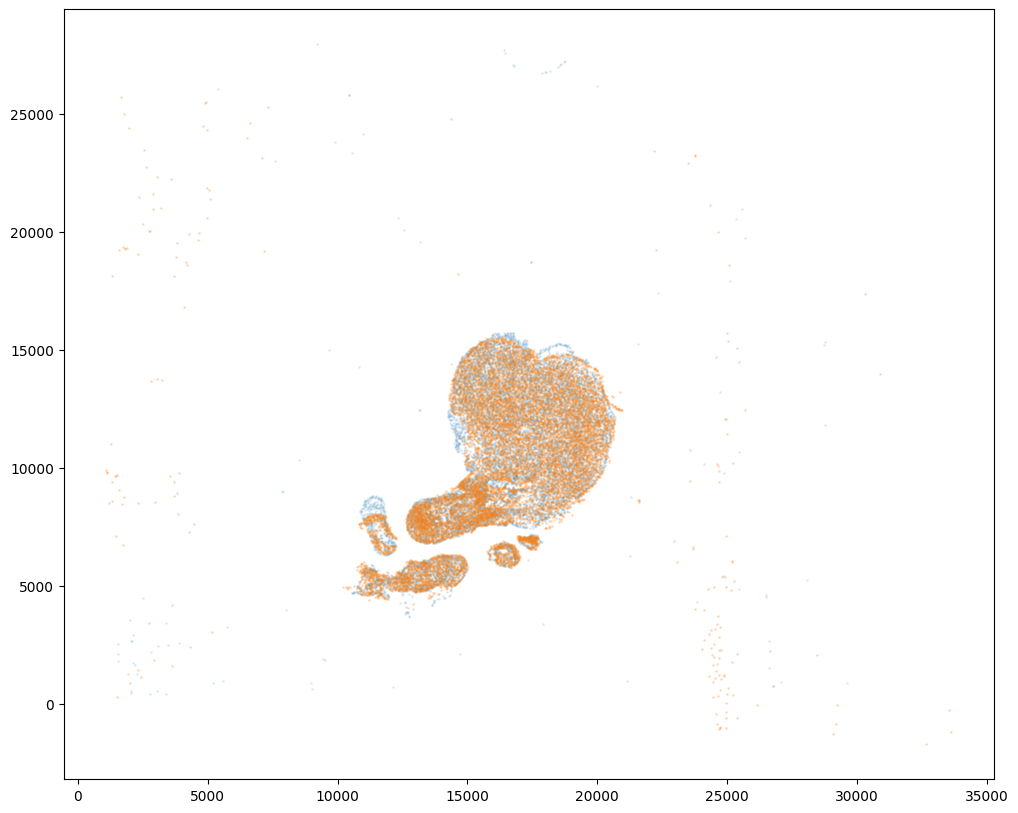
And we can visualize the results.
[17]:
# plot results
fig,ax = plt.subplots()
ax.scatter(tpointsI[0,:],tpointsI[1,:],s=1,alpha=0.1)
ax.scatter(tpointsJ[:,1],tpointsJ[:,0],s=1,alpha=0.2) # also needs to plot as y,x not x,y
[17]:
<matplotlib.collections.PathCollection at 0x7f2ad70c8f40>
[18]:
# save results
results = tpointsJ.numpy()
[ ]:
results.to_csv('../heart_data/CN73_E1_to_CN73_E2.csv.gz',
compression='gzip')